Kapitel 3: Binära taloperationer i mikroprocessorn
3.1 Inledning
I en dator görs aritmetiska operationer i 8 bitar, 16 bitar, 32 bitar eller 64 bitar. Ett tal som 3 i binär är 11. Om operationen ska göras i 8 bitar, anses detta som 00000011; före den med 0 nollor.
För ett binärt tal som 10000101 är den mest signifikanta biten biten längst till vänster. Det är 1 i det här fallet. Den minst signifikanta biten är den extrema biten till höger, som fortfarande är 1, för talet. Den mest signifikanta biten förkortas MSB. Den minst signifikanta biten förkortas LSB.
Den BINära siffran förkortas till BIT och skrivs helt enkelt som bit. I talet 10010011 är var och en eller nolla en bit. En grupp om fyra bitar kallas en nibble. En grupp på åtta bitar kallas en byte. En byte består av två nibbles. Den lägre nibblet är nibblet för LSB och det högre nibblet är nibblet för MSB.
En grupp på 8 bitar, 16 bitar, 32 bitar eller 64 bitar kallas ett ord, så länge som den gruppen förmedlar information utöver att bara ange ett tal. Gruppen kallas till exempel ett ord om det är en lågnivåinstruktion i datorn. Det finns också ett ord på 24 bitar, men det är inte vanligt förekommande idag.
Endianness hänvisar till den ordning i vilken byten bildar ett ord. Tänk på 24-bitarsordet – 100100001111010100100010. Detta ord består av tre byte som är:
10010000 11110101 00100010
Den mest signifikanta byten är den längst till vänster. När byten längst till vänster är den mest signifikanta byten och byten längst till höger är den minst signifikanta byten, kallas detta Big Endian-representationen av ordet. Little Endian-representationen är motsatsen.
Datorminnet är en serie celler och varje cell innehåller en byte. Den första cellen i datorns minne är för byte 0, den andra är för byte 1, den tredje är för byte 2, och så vidare. Med big endianness och för det föregående ordet lagras den mest signifikanta byten i byte 0-cell, den mellersta byten lagras i byte 1-cell och den minst signifikanta byten lagras i byte 2-cell. Detta betyder att det finns mer signifikanta byte i den nedre minnescellen.
Det föregående 24-bitarsordet kan skrivas i omvänd ordning av bytes enligt följande:
00100010 11110101 10010000
Nu är den minst signifikanta byten längst till vänster och den mest signifikanta byten är längst till höger. När byten längst till vänster är den minst signifikanta byten och byten längst till höger är den mest signifikanta byten, är det Little Endian-representationen av ordet. Med liten endianness och för det föregående ordet lagras den minst signifikanta byten i byte 0-cellen, den mellersta byten lagras i byte 1-cellen och den mest signifikanta byten lagras i byte 2-cellen. Detta betyder att det finns mindre signifikant byte i den nedre minnescellen.
Endianness används inte för bitar i en byte. Det används inte heller för nibbles i en byte. Den används bara för byteordning.
Nummerraden
Ett tal utan tecken är ett positivt tal. Positiva tal är tal från noll som går uppåt. Negativa tal finns också. Positiva och negativa tal kan presenteras på en tallinje. Följande tallinje visar de positiva och negativa heltal (heltal) nära noll:
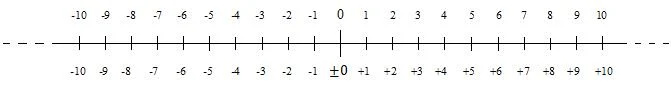
Negativa tal minskar från noll och nedåt (vänster). I många situationer anses noll vara positivt. Det anses dock vara negativt i vissa situationer. Det är därför det finns ett plus- och minustecken framför noll, i den lägre numreringen, i diagrammet. När en siffra är positiv kan dess tecken utelämnas; detta är fallet för den övre numreringen i diagrammet. Minustecknet framför ett negativt tal utelämnas aldrig.
3.2 Addering av binära tal
I tillägget:
A + B = S
A kallas augend, B kallas addend och S kallas summan.
Betrakta följande addition av två positiva tal i bas två:

I bas två är de enda möjliga siffrorna 0 och 1. Addition i bas 2 liknar addition i bas tio, men två i bas två är en-noll (10). När summan av två bitar i en kolumn är 10 skrivs 0 och 1 förs till den omedelbart vänstra kolumnen; läggas till summan av de två bitarna där. När den totala summan är tre betyder det 11 i bas två. Den högra 1 av 11 skrivs och den vänstra 1:an bärs för att läggas till summan av de omedelbara vänstra kolumnbitarna. I båda fallen kallas 1:an som bärs åt vänster för bär.
När man läser den föregående additionstabellen från höger, i den andra kolumnen (från höger), finns en överföring som resulterar från 1+1 = 10. I den tredje kolumnen finns en överföring som är resultatet av 1+1+ överföring av 1 = 11. I den fjärde kolumnen finns en överföring som resulterar från 0+1+ överföring av 1 = 10. I den femte kolumnen finns det ingen överföring eftersom summeringen är 0+0+ bär av 1 = 1. resten av kolumnerna innebär ingen överföring.
Kolumnräkningen börjar från den högra änden. Med 16-bitars addition kan det finnas en överföring från den åttonde kolumnen till den nionde kolumnen (flyttar sig åt vänster). Följande tabell illustrerar detta:

Aritmetiska och logiska operationer sker i mikroprocessorn på datorns moderkort.
För en 8-bitars orddator kan inte bäraren gå från den åttonde biten till den nionde biten automatiskt av hårdvara. Så för att lägga till två 16-bitars grupper i en sådan dator måste tillägget göras två gånger i åtta-åtta bitar. Bärandet flyttas och utförs av programvaran (programmering).
För att lägga till två siffror kan talen konverteras först till deras tvås komplementform (se nedan) innan de läggs till.
3.3 Tvåkomplement och dess subtraktion av binära tal
På datorns moderkort finns minnet och det finns mikroprocessorn och andra kretsar. Minnet är en serie av åttabitarsceller. För en byte går varje bit in i en cell. Mikroprocessorn har några platser av minnestyp. Dessa platser av minnestyp kallas register. Så i datorn kan grupper av byte lagras tillfälligt i minnet eller i mikroprocessorns register.
I någon av dessa lagringar kan varje cell ta antingen en 1 eller en 0, och inget annat. I livet finns det positiva och negativa siffror. Ett positivt tal börjar med ett plustecken (+) och ett negativt tal börjar med ett negativt tecken (-). När tecknet utelämnas betraktas talet som ett positivt tal.
För att lösa detta problem med att ange tecknet för ett tal i datorn lagras de heltal i intervall. Heltal är heltal. Om åtta bitar används för att lagra intervallet av möjliga tal, används biten längst till vänster som teckenbit. Om talet börjar med 0 är talet ett positivt tal. Om det börjar med 1 är talet ett negativt tal. Om sexton bitar används för att lagra intervallet av möjliga tal, används biten längst till vänster som teckenbit. Om talet börjar med 0 är t talet ett positivt tal. Om det börjar med 1 är talet ett negativt tal. Siffrorna i detta formulär kallas undertecknade nummer.
I praktiken kan det finnas signerade nummer för 8 bitar, 16 bitar, 32 bitar och 64 bitar. Ju bredare antal bitar som används, desto större intervall av möjliga nummer som kan lagras.
Tvås komplement heltal
Med tvås komplement är de positiva talen de normala räknetalen, förutom att siffran längst till vänster är 0. För att få motsvarande negativa tal för ett givet positivt tal, invertera varje bit i talet och lägg till 1 till resultatet. Inverteringen eller komplementet av 0 är 1. Inverteringen eller komplementet av 1 är 0. Följande tabeller visar några tvås komplementtal i deras intervall:
| Tabell 3.31 Tvås komplement heltal i två bitar |
|
|---|---|
| Binär | Decimal |
| 01 | +1 |
| 00 | +0 |
| elva | -1 |
| 10 | -2 |
De positiva binära talen är 00 och 01 (det vill säga noll och ett). I biten längst till vänster visar noll att de är positiva tal. 00 är något i mitten av intervallet. För att erhålla -1, visar sig inverteringen av talet 01 vara 10. Lägga till 1 till detta (ytterst till höger) ger 11.
Eftersom två bitar används finns bara en bit kvar för att representera talen i intervallet som består av talen +1, +0 och -1 motsvarande 01, 00 och 11. Den första biten indikerar tecknet. Det händer att 10 för +2 inte är bland dessa tre binära tal. 10 börjar med 1 vilket betyder att det måste vara ett negativt tal i tvås komplement. Så, 10 ingår i intervallet, vilket betyder -2.
Med två bitar i tvåkomplement är antalet av alla heltal (positiva och negativa) som kan representeras 2 2 = 4 och inte 2 2 -1 = 3. Nyansen är resultatet av inkluderingen av det sista negativa talet som är det negativa av 2 nummer med – 1. I detta fall, -2 2-1 = -2 1 = -2. Det finns ingen +2 i intervallet för tvås komplementnummer i 2 bitar.
| Tabell 3.32 Tvås komplement heltal i fyra bitar |
|
|---|---|
| Binär | Decimal |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
De positiva binära talen är från 0000 till 0111 (det vill säga från noll till sju). I biten längst till vänster visar noll att de är positiva tal. 0000 är något i mitten av intervallet. För att erhålla -1, befinns inverteringen av talet 0001 vara 1110. Lägga till 1 till detta (längst till höger) ger 1111. För att erhålla -2, befinns inverteringen av 0010 vara 1101. Lägga till 1 till detta ( från den extrema högern) ger 1110. De andra negativa binära talen som -3 till -7 bestäms på liknande sätt.
Eftersom fyra bitar används lämnas tre bitar kvar för att representera talen i intervallet som är +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 och -7 motsvarande 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1010 och 1001.
Den -8 som motsvarar 1000 måste adresseras separat. Den första biten för alla dessa tal indikerar tecknet 0 för positiva tal och 1 för negativa tal. Det händer att 1000 inte är bland dessa fjorton binära tal. 1000 börjar med 1 vilket betyder att det måste vara ett negativt tal, vad gäller tvås komplement. Så, 1000 ingår i intervallet, vilket betyder -8.
Med fyra bitar i tvåkomplement är antalet av alla heltal (positiva och negativa) som kan representeras 2 4 = 16 och inte 2 4 – 1 = 15. Nyansen härrör från inkluderingen av det sista negativa talet som är det negativa av 2 antalBredd – 1. I detta fall, -2 4 -1 = -2 3 = -8. Det finns ingen +8 i siffrorna.
Den tidigare analysen för två, fyra och bredare bitar i tvås komplement kan tillämpas på 8 bitar, 16 bitar, 32 bitar och 64 bitar breda binära tal.
Tvås komplement offrar den första (längst till vänster) biten för tecknet 0 för positivt tal och 1 för negativt tal. För den 'n' bit breda gruppen av bitar finns det 2 n totalt positiva plus negativa tal. Det skulle bli 2 n -1, om det inte vore för den lyckliga sista (minsta) negativa siffran som ingår. Det högsta positiva talet är +2 n-1 -1 och det minsta negativa talet är -2 n-1 -1. Det skulle bli -2 n-1 -1, vore det inte för den lyckliga -2 n-1 ingår.
Subtrahera siffror i tvås komplement
I subtraktion:
A – B = D
A kallas minuend, B kallas subtrahend och D kallas skillnaden.
För att subtrahera ett positivt binärt tal från ett annat positivt binärt tal, skrivs minuend i tvås komplement och subtrahenden omvandlas till dess negativa tvås komplementvärde. Så det matematiska påståendet blir:
A+ – B = D
Med andra ord, i tvås komplementsubtraktion omvandlas subtrahenden till ett negativt tal och läggs sedan till minuend.
Exempel 3.31:
Utvärdera följande decimaluttryck i tvåkomplement med fyra bitar:
6 – 4
Lösning:
Det binära talet för 6 är 110. I 4-bitars tvåkomplement är det 0110. Det binära talet för +4 är 100. I 4-bitars tvås komplement är det 0100. 0100 som måste omvandlas till negativa 4 i tvåtal. komplement enligt följande: Komplementet eller inversionen av 0100 är 1011. Lägga till 1 till detta från den högra änden, som vi gjorde dessutom, ger 1100. Så, decimaluttrycket är:
6 – 4 som blir:
0110 – 0100 dvs
0110 +(– 0100) = 0110 + 1100 gjort som i föregående tilläggsavsnitt som:

Obs: 0110 +(– 0100) är samma som 6 + – 4
Med tvås komplementsubtraktion slängs alla bär, efter den sista kolumnen åt vänster, i additionen. När man subtraherar med decimal är det matematiska påståendet:
6 – 4 = 2
Om du gör samma sak i tvås komplement, är svaret 0010 vilket är +2 i tvås komplement binär räkning. Den föregående subtraktionen subtraherar ett mindre tal från ett större tal. I följande exempel subtraheras ett större tal från ett mindre tal. Tabell 3.32 kan konsulteras för att se om 0010 verkligen är tvås komplement som motsvarar +2.
Exempel 3.32:
Utvärdera följande decimaluttryck i tvåkomplement med fyra bitar:
4 – 6
Lösning:
Det binära talet för 4 är 100. I 4-bitars tvåkomplement är det 0100. Det binära talet för +6 är 110. I 4-bitars tvås komplement är det 0110. 0110 måste konverteras till negativt 6 i tvåkomplementet enligt följande: Komplementet eller inversionen av 0110 är 1001. Lägga till 1 till detta från den högra änden, som vi gjorde i föregående tillägg, ger 1010. Så, decimaluttrycket är:
4 – 6 som blir:
0100 – 0110 alltså
0100 +(– 0110) = 0100 + 1010 gjort som i föregående tilläggsavsnitt som:

Notera: 4+ – 6 är samma som 0100 +(– 0110).
Med tvås komplementsubtraktion slängs alla bär, efter den sista kolumnen åt vänster, i additionen. När man subtraherar med decimal är det matematiska påståendet:
4 – 6 = -2
Om du gör samma sak i tvås komplement, är svaret 1110 vilket är -2 i tvås komplement binär räkning. Tabell 3.32 kan konsulteras för att se om 1110 verkligen är tvås komplement vilket motsvarar -2.
3.4 Multiplikation av binära tal
I uttalandet:
A x B = P
A kallas multiplikanten, B kallas multiplikatorn och P kallas produkten. A x B-uttrycket betyder att addera A, B antal gånger när A och B är heltal (hela tal).
Multiplikation i binär är detsamma som multiplikation med decimal. Men istället för att göra det i decimaler, görs det binärt. Multiplikationen av decimaluttrycket på 42 x 10 görs binärt enligt följande där 42 10 = 101010 2 och 10 10 = 1010 2 :
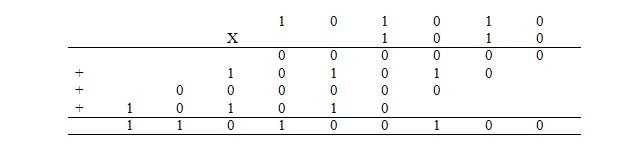
De 4 siffrorna som läggs till betecknas som delprodukter. Svaret är produkten. Tillsatsen av delprodukterna görs på samma sätt som förklarats tidigare.
Multiplikationen kan också ses på följande sätt: I denna bas två multiplikation, om biten (siffran) i multiplikatorn är 1, är den minst signifikanta biten av dess partiella produkt den minst signifikanta biten av multiplikationen som återskrivs direkt under den; och resten av bitarna i multiplikanden upprepas åt vänster. I denna bas två-multiplikation, om biten (siffran) i multiplikatorn är 0, består dess delprodukt av nollor med den minst signifikanta biten noll direkt under sig. Antalet av alla nollor är antalet bitar i multiplikaden.
3.5 Division av binära tal
I uttalandet:
A ÷ B = Q
A kallas Dividend, B kallas Divisor och P kallas Quotient. Kvoten kan åtföljas av en rest. A ÷ B-uttrycket betyder hur många gånger B kan läggas till för att ge A eller vara nära det så att resten är 0 eller mindre än B.
Uppdelning kan göras på många sätt. Indelningen som visas här är restaureringsindelningen.
Återställande division
Detta är den långa divisionsmetoden som man lär sig i skolor. Om 237 delas med 6 är svaret 39 resterande 3. De 237 10 i bas 2 är 11101101 2 och 6 10 i bas 2 är 110 2 . Den 39 10 i bas 2 är 100111 2 och 3 10 i bas 2 är 11 2 .
Så, 11101101 2 dividerat med 110 2 ger 100111 2 resten 11 2 i bas två. Med återställningsmetoden är de binära talen vanliga tal och de är inte nödvändigtvis i tvåkomplement. Följande struktur delar 11101101 2 med 110 2 att ge 100111 2 resten 11 2 :

Subtraktion görs normalt och inte genom att använda de tvås komplement. Eftersom detta är bas två är ett lån två och inte tio. Delutdelningarna är 10, 101, 1011, 1010 och 1001. 11 är resten. Eftersom divisorn har tre siffror görs uppdelningen i princip i grupper om tre siffror från den givna utdelningen. Kvoten är hela talet (heltal), och det är 100111 för detta problem. Kvoten och restresultatet är som förväntat.
3.6 Aritmetiska operationer med programvara och hårdvara
Datorns moderkort har en klocka. Klockans tickar kallas pulser. Vid varje klockpuls tas ett eller flera beslut på olika ställen på moderkortet; och det har att göra med programmering (mjukvara).
Inuti mikroprocessorn finns det två typer av kretsar som kallas: Combinational Logic Circuits och Sequential Logic Circuits. Det finns en annan typ av krets som kallas en multiplexer. Addition, multiplikation och division kan ske inom ett klockintervall med hjälp av kombinationslogiken (kretsen). Medan programmering (mjukvara) begår beslut vid varje klockpuls med hjälp av de sekventiella logikkretsarna och multiplexorerna.
När subtraktion görs med tvås komplement krävs minst två klockpulser. Vid den första klockpulsen kanaliserar en multiplexor subtrahenden till en uppsättning NOT-grindar (en NOT-grind per siffra). Vid den andra klockpulsen adderar kombinationslogiken 1 till utgången från NOT-grindarna och fortsätter att addera den resulterande subtrahenden och minuend. Allt det tillägget kan ske inom ett klockintervall.
Addition, multiplikation och division kan fortfarande vara nere med programmering med hjälp av sanningstabellerna. Det täcks dock inte av denna online karriärkurs.
3.7 Logiska operationer i mikroprocessorn
AND, OR, XOR och Invert
OCH
Följande tabell illustrerar Bitwise AND. Detta betyder att för två olika binära tal OCH-behandlas motsvarande bitar baserat på AND-sanningstabellen:
Flytta från vänster till höger, 1 OCH 1 = 1; O OCH 1 = 0; O OCH O = 0; 1 OCH O = 0; och så vidare i enlighet med AND Sanningstabellen.
ELLER
Följande tabell illustrerar Bitwise OR. Detta betyder att för två olika binära tal, är motsvarande bitar ORed baserat på OR Sanningstabellen:

Flytta från vänster till höger, 1 ELLER 1 = 1; O ELLER 1 = 1; 0 ELLER 0 = 0; 1 ELLER 0 = 1; och så vidare i enlighet med OR Sanningstabellen.
FRI
Följande tabell illustrerar Bitwise exklusiv-ELLER. Detta betyder att för två olika binära tal är motsvarande bitar XORed baserat på XOR Truth-tabellen:

Flytta från vänster till höger, 1 XOR 1 = 0; 0 XOR 1 = 1; 0 XOR 0 = 0; 1 XOR 0 = 1; och så vidare i enlighet med XOR Truth Table.
Invertera (INTE)
Följande tabell illustrerar Bitwise NOT (invertera). Detta innebär att för ett binärt tal, denna gång, inverteras varje bit baserat på NOT Truth-tabellen:

Flytta från vänster till höger, INTE 1 = 0; INTE 0 = 1; INTE 0 = 1; INTE 1 = 0; och så vidare i enlighet med NOT Truth Table.
Växla höger eller vänster
Skift åt höger
Följande binära tal flyttas 3 bitpositioner åt höger, med nollorna infogade i de lediga bitpositionerna till vänster:

Växlingen kan göras för en, två, tre, fyra, etc. platser.
Skift åt vänster
Följande binära tal flyttas 3 bitpositioner åt vänster, med nollorna infogade i de lediga bitpositionerna till höger:

Växlingen kan göras för en, två, tre, fyra, etc. platser.
Roterar höger eller vänster
Att rotera liknar växling. Det görs en bit i taget. När man roterar åt höger, faller inte bitarna som lämnar den högra änden av som vid växling; de ersätter de lediga bitarna till vänster, en efter en. När man roterar åt vänster, faller inte bitarna som lämnar den vänstra änden av som vid växling; de ersätter de lediga bitarna till höger, en efter en.
Vrid höger
Följande binära tal roteras 3 bitars positioner åt höger:

Vridningen kan göras för en, två, tre, fyra, etc. platser.
Rorate vänster
Följande binära tal roteras 3 bitars positioner åt vänster:

Vridningen kan göras för en, två, tre, fyra, etc. platser.
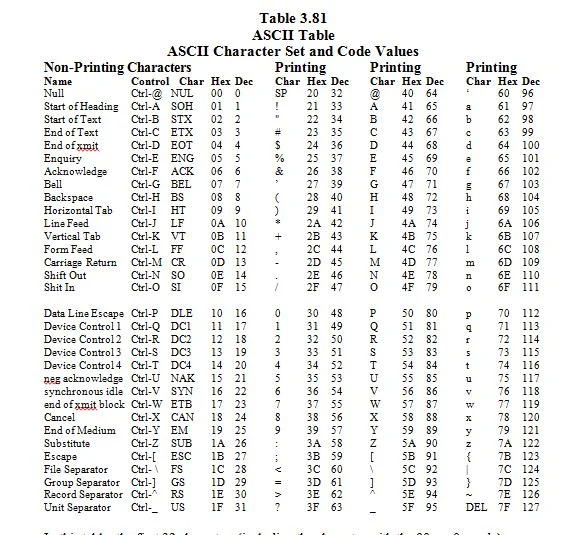
3.8 ASCII-teckenuppsättning och dess kodvärden
ASCII står för 'American (U.S.A) Standard Code for Information Interchange'. Föreställ dig ett tangentbord med 96 tangenter. Detta är ett idealiskt tangentbord där knapparna med stora bokstäver skiljer sig från tangenterna för gemener. Varannan tangent representerar ett tecken som finns på ett engelskt (U.S.A) tangentbord. Tecknen och koderna (motsvarande siffror för tecknen) listas i följande:
I den här tabellen, de första 32 tecknen (inklusive tecknet med 00 16 = 0 10 kod) är tecken som inte kan skrivas ut. De är kontrollkaraktärer. De syns inte på skärmen (monitorn) där allt är lika. De har bara effekter. Låt oss diskutera mer om det senare.
Resten av tecknen är utskriftstecken; de syns på skärmen. Det finns 128 ASCII-tecken. 2 7 = 128. 1,111,111 2 = 127 10 . 7 i 2 7 betyder 7 bitar.
Nu, 1111111 2 + 1 2 är det samma som:
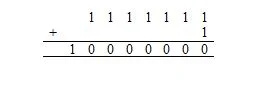
Här, 10 000 000 2 = 128 10 . Det finns 128 10 tecken i föregående lista (tabell) med ASCII-tecken. Detta inkluderar nolltecknet, vars kod i bas sexton (hexadecimal) är 00, vilket motsvarar 0 i bas tio.
Eftersom det finns 128 tecken totalt ger 128 minus 32 tecken som inte är utskrivna 96 tecken för utskrift. I det här avsnittet antas det att det finns ett idealiskt tangentbord med 96 tecken som är utskrivbara tecken. På detta idealiska tangentbord skiljer sig tangenterna för de engelska versalerna från tangenterna för de engelska gemena tecknen.
Varje tecken på tangentbordet representeras av ett basnummer på 7 bitar som inte visas i listan. Den stora bokstaven i 'N', till exempel, representeras av de sju bitarna 1001110 i bas 2. För att konvertera 1001110 2 till bas 16, föregå den med 0 och gruppera resultatet i fyra-bitars undergrupper enligt följande:
| 0100 | 1110 | 2 = | 4 | E | 16
Det är 01001110 2 = 4E 16 . För att konvertera 4E 16 för att basera tio, gör följande:
4 x (16) 1 + E x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
Till höger om 'N' i listan (tabell) finns hexadecimaltalet 4E och decimaltalet 78.
Som ett annat exempel representeras tecknet '[' av de sju bitarna 1011011 i bas 2. För att konvertera 1011011 2 till bas 16, föregå den med 0 och gruppera resultatet i fyra-bitars undergrupper enligt följande:
| 0101 | 1011 | 2 = | 5 | B | 16
Det är 01011011 2 = 5B 16 . För att konvertera 5B16 till bas tio, gör följande:
5 x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
Till höger om '[' i listan (tabell) finns det hexadecimala talet 5B och decimaltalet 91.
Som ytterligare ett exempel representeras tecknet för decimaltalet '5' av de sju bitarna 0110101 i bas 2, och inte 0000101 i bas 2. För att konvertera 0110101 2 till bas 16, föregå den med 0 och gruppera resultatet i fyra-bitars undergrupper enligt följande:
| 0011 | 0101 | 2 = | 5 | B | 16
Det är 00110101 2 = 35 16 . För att konvertera 3516 till bas tio, gör följande:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
Till höger om '5' i listan (tabell) finns hexadecimaltalet 35 och decimaltalet 53.
Eftersom datorn fungerar i byte, när en tangent på det ideala tangentbordet trycks ned, skickas åtta bitar till mikroprocessorn (moderkortet). Det ideala tangentbordet är en kringutrustning som är skild från datorns systemenhet (bas). Den har en elektronisk krets (IC) som skapar de sju bitarna och föregår den med en nolla innan den skickas genom kabeln till systemenhetens moderkort. Från ingångsporten (ingångskretsen) på moderkortet går den till mikroprocessorn som också finns på moderkortet. Från mikroprocessorn går den till minnet som även sitter på moderkortet.
Så när 'N'-tangenten på det ideala tangentbordet trycks ned, tas åtta bitar 01001110 till mikroprocessorn. Från mikroprocessorn tas de till minnet där de förblir på en minnesplats som en byte. Datorprogrammeraren bör komma ihåg att de åtta bitarna i 01001110 2 är samma som 4E 16 vilket är samma som 78 10 .
När '['tangenten på det ideala tangentbordet trycks in, tas åtta bitar 01011011 till mikroprocessorn. Från mikroprocessorn tas de till minnet där de förblir på en minnesplats som en byte. Datorprogrammeraren bör komma ihåg att de åtta bitarna i 01011011 2 är samma som 5B 16 vilket är samma som 91 10 .
När '5'-tangenten på det ideala tangentbordet trycks ned, som ett tecken och inte som decimaltal, tas åtta bitar 00110101 till mikroprocessorn. Från mikroprocessorn tas de till minnet där de förblir på en minnesplats som en byte. Datorprogrammeraren bör komma ihåg att de åtta bitarna i 00110101 2 är samma som 35 16 vilket är samma som 5310 10 .
Det finns tillfällen då ett program körs och väntar på att decimaltalet 5 ska matas in i datorn. I den här situationen, om '5'-tangenten på det ideala tangentbordet trycks ned, tas fortfarande åttabitarskoden 00110101 till mikroprocessorn. Eftersom det som behövs är decimaltalet 5, och inte '5'-tecknet, använder en bit kod (kort program) från minnet mikroprocessorn för att konvertera teckenkoden för 00110101 i bas två till de tvås komplementnummer 00000101 2 innan du skickar den till en minnesplats som en tvåkomplementbyte. Datorprogrammeraren måste komma ihåg att 00000101 betyder 5 10 i bas 2, och det skiljer sig från kodnumren för 00110101 2 , 35 16 och 53 10 vilket betyder tecknet '5'. För att visa de tvås komplementnummer 00000101 i minnet måste ett annat kort program konvertera 00000101 från minnet till 00110101. Det är 00110101 vilket är samma som 35 16 vilket är samma som 53 10 som visas på monitorn (eller skrivs ut på ett papper av skrivaren).
3.9 Flyttalsformat
Ett tal utan en decimaldel är ett heltal. Siffran 36 är ett heltal. 36.375 är inte ett heltal. Det är ett decimaltal med en decimaldel. Decimaldelen av .375 är en bråkdel som är mindre än 1.
36,375 tolkas i decimalform som:
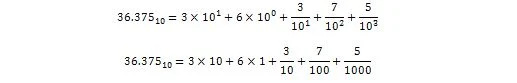
Nu:
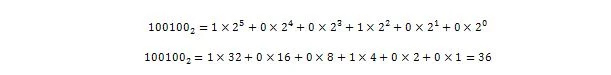
Alltså 100 100 2 = 3610 vilket är hela taldelen av 36,375 10 .
Nu:
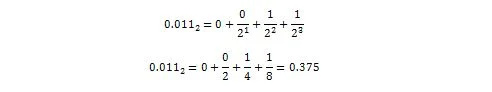
Alltså 0,011 2 = 0,375 10 vilket är decimaltalet del av 36,375 10 .
∴ 36 375 10 = 100100,011 2
Uttryckt på ett annat sätt:
100100.011 2 = 36,375 10
Tal representeras i datorn i bas 2 och inte i bas 10, med allt lika. Eftersom en cell i ett register i mikroprocessorn eller en cell i minnet bara kan ta 1 eller 0, finns det inget utrymme att lagra en decimalkomma. Detta utgör ett problem. Som upplösning finns IEEE-754 enkelprecision 32-bitars flyttalsrepresentation och IEEE-754 dubbelprecision 64-bitars flyttalsrepresentation.
32-bitars flyttalsformat
Numret 100100.0112 kan uttryckas som:
100100.011 2 = 1,00100011 2 x 2 +5
Den högra sidan av symbolen = hänvisas till i matematik som grundformen två av den vänstra sidan av 100100.011 2 .
Nu, 00100011 av 1,00100011 2 på höger sida om symbolen =, utan föregående '1'. och utan 2:an för basen, kallas den explicita signifikanden. I det här fallet tas den binära punkten fem platser till vänster för att få '1'. Blanda inte ihop decimalkomma och binär komma. Binär punkt är för bas 2, medan decimalpunkt är för bas 10. '1'. följt av 00100011 på höger sida om symbolen =, utan 2:an för basen, bildar den sanna signifikansen. Emellertid kallas 1,00100011 den implicita signifikanden.
Efter signifikansen på höger sida är 'x 2 +5 ' uttryck. Med detta uttryck kallas +5 för exponenten. Plustecknet betyder att den binära punkten måste flyttas fem platser framåt för att vara i sin normala ursprungliga position och 2 är basen för numreringen. Den föregående ekvationen kan skrivas omvänt som:
1,00100011 2 x 2 +5 = 100100,011 2
Med 32-bitars flyttalsrepresentation är det '1.00100011 2 x 2 +5 ” som används och inte bara ”100100.011 2 ”. 2:an för basen registreras inte. 32-bitars flyttalsrepresentation för '1.00100011 2 x 2 +5 ” nummer, vilket är lika med 36,375 10 = 100100,011 2 , visas i följande tabell:

Det finns 32-bitars positioner som är numrerade från den högra änden, med början från 0. Den första biten på den vänstra änden är teckenbiten. Om talet är positivt är denna bit 0. Om talet är negativt är denna bit 1 (-1 består av två tecken och kan inte placeras i någon cell). Den 1,00100011 2 x 2 +5 vilket är lika med 36,375 10 vilket också är lika med 100100,011 2 är ett positivt tal. Så den första biten är 0.
Det finns åtta bitpositioner för exponenten, med början från position 30 till position 23 inklusive. Exponenten som skrivs där är dock 10000100 2 vilket är lika med 132 10 . Exponenten för antalet intressen är faktiskt +5 av basen av två. Så vad händer?
Nu, i 32-bitarsformatet, skrivs en exponent av 0 som 01111111 2 vilket är lika med 127 10 . +5:an 10 är +101 2 . Så när jag kommer fram till 10000100 2 i exponentdelen i tabellen, 101 2 lades till 01111111 2 , motsvarande. Det betyder att 5 lades till 127 för att ha 132 10 .
Signifikanden, utan '1', tog positionerna 22 ner till 15, inklusive. Observera att 1:an av '1.' har inte indikerats i 32-bitarssträngen. Det anges aldrig – acceptera det. Resten av cellerna ner till position 0 är fyllda med nollor.
Om den faktiska exponenten är -5, subtraheras 5 från 127 10 att ha 122 10 . Detta motsvarar att subtrahera 101 2 från 01111111 2 att ha 01111010 2 .
Med alla föregående illustrationer, talet +1 som är lika med 1,0 x 2 0 = 1,0 x 1 = 1,0 representeras som:

Observera att '1.' på 1,0 x 2 0 anges inte i formatet. Det anges aldrig. Nästa blandade fraktion som går positivt efter 1,0 är:

Lägg märke till 1:an till höger. Denna representation är numret:

Skillnaden mellan 1,0000001192092896 och 1,0 är:
1,0000001192092896 – 1,0 = 0,0000001192092896
Siffrorna med decimaldelar är blandade bråk. Inte alla bråken mellan 1 10 och 2 10 kan representeras i datorn. Det kan antas att det minsta bråktalet mellan de på varandra följande blandade talen med 32-bitars flyttalsformat är 0,0000001192092896. Räkna med att intervallet för dubbel precision är mindre. Se följande illustration.
Representerar talet, 0,0 följer inte de tidigare argumenten. Representationen för 0,0 deklareras och måste läras in som sådan. För att representera 0,0 är alla celler för signifikanden 0 och alla celler för exponenten är också noll. Teckenbiten kan vara 0 eller 1. Tyvärr ger detta upphov till positiv 0 och negativ 0 enligt följande:

I verkliga livet finns det bara en nolla. Positiv 0 och negativ 0 finns inte. Men 0 anses vanligtvis vara positivt. Positiv 0 och negativ 0 finns här på grund av denna speciella formatbeskrivning. Tallinjen (se ovan) kan också ha +0 och -0, men det finns bara en nolla.
64-bitars flyttalsformat
64-bitars flyttalsformatet liknar 32-bitarsformatet, men med följande skillnader:
- Det finns 64 bitar för att representera ett tal.
- Efter teckenbiten finns det 11 bitar för exponentnumret.
- Exponentnumret för nollindex (2 0 ) är 1023 10 = 01111111111 2 .
- De elva bitarna följs av 52 bitar för den explicita signifikanden.
- Den har ett bredare antal nummer än 32-bitarsformatet.
Observera att '1.' som är i början av signifikanden är fortfarande inte inkluderad bland de 64 bitarna, precis som den inte ingår bland de 32 bitarna för 32-bitarsformatet.
En av de viktigaste skillnaderna mellan 64-bitarsformatet och 32-bitarsformatet är att skillnaden mellan de på varandra följande blandade bråken i 64-bitarsformatet är mindre än för 32-bitarsformatet.
I 64-bitarsformatet kan intervallet (gapet) mellan 1,0 och nästa blandade fraktion beräknas enligt följande:
1,0 är
0 01111111111 000000000000000000000 00000000000 00000000000000000000000 2
Detta motsvarar '1.', som inte har indikerats i strängen, multiplicerat med 2 upphöjt till potensen (index) 0 (med exponenten är 1023 10 = 01111111111 2 för 2 0 = 1). Snöret är 1,0 x 2 0 .
Nästa blandade fraktion större än 1,0 är:
0 01111111111 000000000000000000000 00000000000 000000000000000000000001 2
Detta motsvarar '1'. som inte anges i strängen, följt av 51 nollor, och sedan 1, multiplicerat med 2 upphöjt till potensen 0 (med exponenten är 1023 10 = 011111111112 2 för 2 0 = 1). Detta är samma sak som:
+2 0 × (1 + 2− -52 ) ≈ 1,00000000000000002
≈ betyder ungefär lika med.
Nu:
1,00000000000000002 – 1,0 ≈ 0,00000000000000002
Motsvarande intervallvärde för ett 32-bitars format är 0,0000001192092896 ≈ 0,00000012.
0,00000000000000002 är mycket mindre än 0,00000012. Så det finns mycket fler blandade bråk mellan två på varandra följande heltal (t.ex. 3 och 4) i 64-bitarsformatet än det finns mellan två på varandra följande heltal för 32-bitarsformatet.
Antalet blandade bråk mellan två på varandra följande heltal på tallinjen är oändligt. Så inget format (t.ex. 32-bitars eller 64-bitars) kan tillhandahålla alla de blandade bråken mellan två på varandra följande heltal (heltal). Ju mindre gapet (intervallet) mellan två på varandra följande heltal tillhandahålls av ett format (t.ex. 32-bitars eller 64-bitars), desto större är antalet blandade bråk mellan de på varandra följande heltal (för tallinjen).
Anledningarna till att 64-bitarsformatet beskrivs som dubbel eller högre precision, jämfört med 32-bitarsformatet, är att intervallet mellan två på varandra följande blandade bråk avgränsade av två på varandra följande heltal för 64-bitarsformatet är mindre än motsvarande 32 -bitformatsintervall. Det finns också fler möjliga blandade bråk mellan två avgränsade heltal för 64-bitarsformatet än det finns på motsvarande sätt för 32-bitarsformatet.
Konvertera en decimaldel (bråkdel) av decimaltal till en binär del
36.375 är ett decimaltal med decimaldelen '.375'. Decimaldelen av '.375' är en bråkdel mellan noll och ett. 0,5 i bas tio är samma värde som 1/2 i bas två. Den 0,5 10 som uttrycks med bas två-expansionen är:
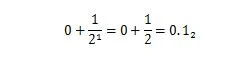
Det är inte 0,101 2 vilket betyder 0,625 10 . Decimaldelen av ett decimaltal har sin motsvarande binära del för motsvarande binära tal. Så, för att konvertera ett decimaltal som 36,375 10 för att basera två, konvertera 36 till binär och sedan konvertera .375 också till binär. Slå sedan ihop båda resultaten med den binära punkten. Metoderna för att konvertera de två sektionerna är olika. Hur man konverterar ett decimalt heltal till bas 2 förklaras i kapitel 1.
För att konvertera decimalbråket till binärt bråk, följ följande steg:
- Multiplicera decimalbråket (decimaldelen) med 2. Heltalet som blir resultatet av detta är den första binära siffran.
- Upprepa föregående steg med bråkdelsdecimalresultatet för att få nästa binära siffra.
- Fortsätt att upprepa föregående steg tills decimalresultatet är 0,0000—.
Exempel: Konvertera bråkdelen av 36,375 10 till motsvarande bråkdel i bas två.
Lösning:
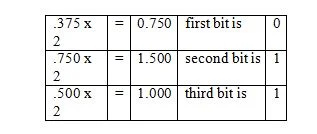
Observera att i det tredje steget multiplicerades .500 med 2 och inte 1.500. Den binära motsvarande fraktionen läses i den sista kolumnen uppifrån. Och så är följande resultat:
.375 10 = .011 2
Konvertera en binär del (bråkdel) av binärt tal till en decimaldel
För att uppnå detta, expandera den binära bråkdelen i ömsesidiga potenser av 2.
Exempel: Konvertera bråkdelen av 100100.011 2 till motsvarande bråkdel i bas tio.
Lösning:
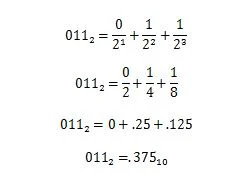
3.10 Nummerprefix i datoranvändning
I normalt liv betyder 1 kilo 1000 vilket förkortas i k (gemener) som i 1kg. I beräkning betyder 1 kilo 2 10 = 1024, men förkortas i K (versaler) som i 1Kbits. I det normala livet betyder 1 mega 1 000 000 som förkortas i M (versaler) som i 1Mg. I beräkning betyder 1 mega 2 tjugo = 1 048 576 = 2 10 x 2 10 = 1024 x 1024 = 1 048 576 och förkortas fortfarande i M (versaler) som i 1Mbits. I det normala livet betyder 1 giga att 1 000 000 000 förkortas i G (versaler) som i 1Gg. I beräkning betyder 1 giga 2 30 = 1 073 741 824 = 2 10 x 2 10 x 2 10 = 1024 x 1024 x 1024 = 1 073 741 824 och förkortas fortfarande i G (versaler) som i 1 Gbit. Följande tabell ger betydelsen av fyra prefix i det normala livet och i datoranvändning:
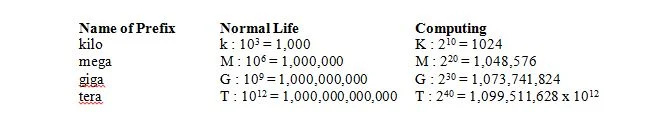
3.11 Problem
Läsaren rekommenderas att lösa alla problem i ett kapitel innan du går vidare till nästa kapitel.
- Rita en tallinje med heltal från -10 till +10.
- Lägg till följande binära tal i 8-bitars tvåkomplement: 101010 2 och 1111 2 .
- Använd endast tvåkomplementmetoden i 8-bitar för att subtrahera det binära talet 1111 2 från det binära talet 101010 2 .
- Hitta produkten från 10110 2 x 1101 2 i bas två.
- Dela 36 375 10 med 1000 10 i decimal och binär, och jämför resultaten.
- Använd de 8-bitar du väljer för att illustrera de logiska OCH, ELLER, XOR, Invertera, Skift höger, Skift vänster, Rotera höger och Rotera vänster. Varje byte bör ha en blandning av 1:or och 0:or.
- a) Skriv den numeriska koden för ASCII-tecknet noll i hexadecimal, binär och decimal.
b) Skriv den numeriska koden för ASCII-tecknet '1' i hexadecimal, binär och decimal.
c) Skriv den numeriska koden för ASCII-tecknet 'A' i hexadecimal, binär och decimal.
d) Skriv den numeriska koden för ASCII-tecknet för 'a' i hexadecimal, binär och decimal. - Konvertera 49,49 10 in i bas två. Konvertera ditt resultat till IEEE 32-bitars flyttalsformat.
- a) Hur skiljer sig IEEE 64-bitars flyttalsformat från 32-bitarsformatet?
b) Ge de två relaterade anledningarna till varför 64-bitarsformatet beskrivs som dubbel eller högre precision över
32-bitars format.