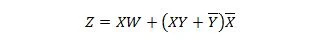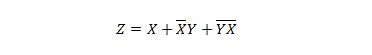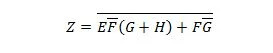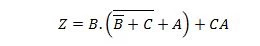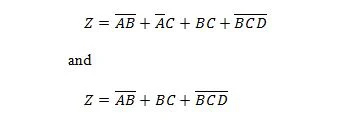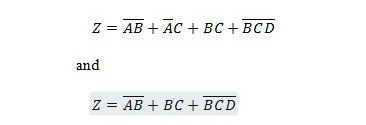Kapitel 2: Boolesk algebra och dess relaterade datorkomponenter
2.1 Grundläggande booleska operatörer
Antag att jag (författaren) är lång och du (läsaren) är lång. Om någon frågar dig om vi båda är långa, skulle du säga 'Ja' (sant). Om han frågar om vi båda är korta, skulle du säga 'Nej' (falskt). Om du är kort och jag är lång, och han frågar dig om antingen du eller jag är lång, skulle ditt svar vara 'Ja' (sant). Om han frågar om både du och jag är långa skulle du inte ha något svar. Du kan fortsätta med att säga att den sista frågan inte ska ställas eller att frågan inte har något svar. Jo, jag vill att du (läsaren) ska veta att i dag, under vissa omständigheter, bör frågan ställas.
Inom biologi är en person antingen lång eller kort. Det är de ”miljömässiga” förhållandena som gör att personen har medellängd. En vetenskapsman, George Boole, definierade en uppsättning svar eller regler för denna typ av frågor. Vi kommer att lära oss dessa regler i det här avsnittet av onlinekarriärkursen (kapitel). Dessa regler används idag inom datorer, programmering, elektronik och telekommunikation. Faktum är att utan dessa regler skulle du inte ha en dator, som det är vanligt idag; du skulle inte också ha programmering, som det är vanligt idag.
Sant eller falskt
Ett enkelt mänskligt språkpåstående är antingen sant eller falskt i sig. Om jag säger 'Jag är lång', är det antingen sant eller falskt. Om jag säger 'du är lång', är det antingen sant eller falskt. Om jag är lång och du är kort, och frågan ställs om både du och jag är långa, i boolesk logik måste svaret sant eller falskt ges. Vilken av dessa två ska ges? Boole svarade inte riktigt på denna fråga. Han kom helt enkelt på en uppsättning regler som vi skulle följa. Den goda nyheten är att när du följer dessa regler i deras rätta sammanhang, har du ingen tvetydighet. Tack vare dessa regler har vi idag datorer och programmering. Reglerna ges till dig nu. Reglerna kan inte riktigt förklaras; du bara accepterar dem. Reglerna finns under tre rubriker: OCH, ELLER och INTE.
OCH
Frågan kan ställas om både du OCH jag är långa. Min längd och din längd kombineras sedan av OCH-reglerna. Det här är OCH-reglerna att följa:
false AND false = falskt
falskt OCH sant = falskt
sant OCH falskt = falskt
sant OCH sant = sant
Låt nu lång vara sann och kort vara falsk. Det betyder att om jag är kort OCH du är kort så är du och jag korta. Om JAG är kort OCH du är lång, är du och jag korta; det är det booleska svaret som du måste acceptera. Om jag är lång OCH du är kort så är både du och jag korta. Om jag är lång OCH du är lång så är du och jag långa. Allt detta är OCH booleska regler som du (läsaren) bara måste acceptera.
ELLER
Frågan kan ställas om du ELLER jag är lång. Min längd och din längd kombineras sedan av ELLER-reglerna. Dessa är OR-reglerna att följa:
false OR false = false
falskt ELLER sant = sant
sant ELLER falskt = sant
sant ELLER sant = sant
Återigen, låt lång vara sann och kort vara falsk. Det betyder att om jag är kort ELLER du är kort så är du ELLER jag kort. Om jag är kort ELLER du är lång, är du eller jag lång. Om jag är lång ELLER du är kort så är du ELLER jag lång. Om jag är lång ELLER du är lång så är du eller jag lång. Alla dessa är booleska regler som du måste acceptera.
INTE
Nu, i boolesk logik, existerar bara två tillstånd (möjliga svar). Det vill säga om du INTE är lång så är du kort. Om du INTE är kort är du lång; inget annat. Dessa är INTE-reglerna att följa:
INTE falskt = sant
INTE sant = falskt
Antag att du har ett snöre (eller fjäder) som du kan förlänga (dra). Medan strängen är i sitt naturliga tillstånd, om jag säger 'INTE kort', skulle du förlänga den; det är tolkningen. Medan strängen är förlängd, om jag säger 'INTE lång', skulle du låta den dra ihop sig; det är tolkningen.
Du måste memorera alla givna regler i deras olika kategorier.
Mer än två operander
I ett datorspråk kallas AND, OR och NOT var och en för en operator. För NOT-operatorn behöver du bara en operand (värde för en operator) för att få ett svar. För operatorerna OCH eller ELLER kan du ha fler än två operander. De tidigare fallen visar två operander för AND och OR. Du kan ha tre operander för AND enligt följande:
false AND false AND false = falskt
false AND false AND true = falskt
Det här är två rader; var och en har två AND-operatorer. Det finns faktiskt nio rader när operanderna är tre. Med AND-operatorn är endast den sista raden (nionde raden) lika med sant; alla föregående rader är falska. Observera att med två operander för AND är bara den sista raden sann fortfarande; alla de tre föregående raderna är falska. När operanderna är fyra finns det 16 rader och endast den sista raden är sann för OCH-operatorn.
Mönstret för OCH och mönstret för ELLER är olika. Med tre operander för två ELLER-operatorer finns det också nio rader och endast den första raden, denna gång, är falsk. Den andra till den nionde raden är sann. Observera att med två operander för ELLER är endast den första raden sann fortfarande; alla de återstående tre raderna är falska. När operanderna är fyra för ELLER finns det också 16 rader.
NOT-operatorn hanterar endast en operand. INTE falskt är sant och INTE sant är falskt.
2.2 Två operande sanningstabeller och deras elektroniska komponenter
Inom matematiken finns det ett ämne som kallas algebra. En liten del av det sågs i föregående kapitel. Det finns en sorts algebra som kallas boolesk algebra. I boolesk algebra identifieras sant av basen två siffran som är 1 och false identifieras med basen två siffran som är 0.
De interna datorenheternas komponenter är elektroniska komponenter. Datorsystemets systemenhet har digitala elektroniska komponenter. OCH-operationen görs av en liten elektronisk komponent som kallas OCH-grinden. ELLER-operationen görs av den lilla elektroniska komponenten som kallas ELLER-grinden. NOT-operationen görs av den lilla elektroniska komponenten som kallas NOT-grinden. För många av dessa grindar kan finnas i ett IC-chip (Integrated Circuit).
OCH Sanningsbordet och dess port
Följande tabell ger AND-sanningstabellen och dess AND-grind (liten krets)-symbol:
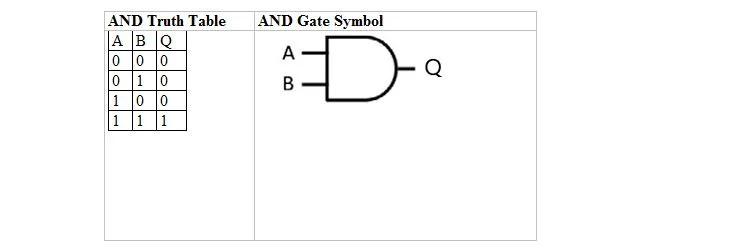
För både AND-sanningstabellen och dess grind är A såväl som B två indatavariabler. Q är utdatavariabeln. A är antingen 1 eller 0. B är antingen 1 eller 0. Q är antingen 1 eller 0. OCH-sanningstabellen med 1:or och 0:or är samma som den tidigare sant/falska OCH sanningslayouten (tabell). OCH-ekvationen är:
A . B = Q
där punkten (.) betyder OCH (boolesk). Punkten kan utelämnas för att ha AB = Q vilket betyder samma sak (OCH).
Obs: Bitarna för A och B i de fyra raderna, som par, är de första fyra talen i bas två som börjar från 0 (eller 00), dvs. 00, 01, 10, 11.
Följande tabell ger ELLER-sanningstabellen och dess ELLER-port (liten krets) symbol:
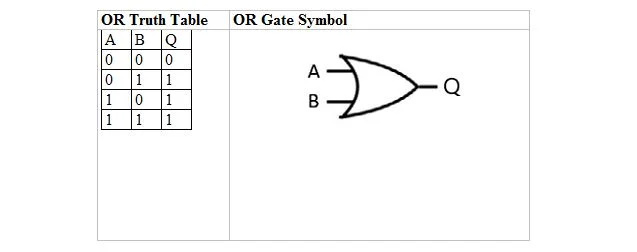
För både ELLER-sanningstabellen och dess grind är A såväl som B två indatavariabler. Q är utdatavariabeln. ELLER-sanningstabellen med 1:or och 0:or är densamma som den tidigare sant/falska ELLER-sanningslayouten (tabellen).
ELLER-ekvationen är:
A + B = Q
Där + här betyder booleskt ELLER och inte addition. Ekvationen läses som 'A eller B lika med Q'.
Följande tabell ger NOT sanningstabellen och dess NOT gate (liten krets) symbol:
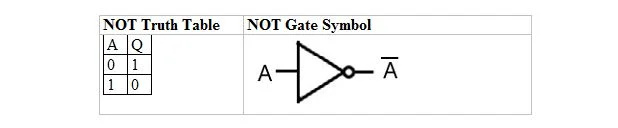
NOT-sanningstabellen eller NOT-grinden har bara en ingång och en utgång. När ingången är 0 är utgången 1. När ingången är 1 är utgången 0. NOT-grinden gör en slags invertering. Utdatavariabeln är densamma som indatavariabeln, men med en stapel (överrad). NOT-sanningstabellen med 1:or och 0:or är densamma som den tidigare sant/falska ELLER sanningslayouten (tabellen).
NOT-ekvationen är:
A = Q
Där Q = A och stapeln över A betyder här komplement. Komplementet av 0 är 1 och komplementet till 1 är 0. NOT-grinden är också känd som INVERTERANDE grind.
Dessa är de fundamentala (eller rot-) sanningstabellerna och deras grindar (små kretsar) i digital elektronik (med boolesk algebra). De andra tre sanningstabellerna som ges i följande illustration och deras portar är för bekvämlighet och är baserade på de tre föregående sanningstabellerna.
Det finns en sanningstabell och grind som härleds från AND-sanningstabellen och -porten. De kallas NAND (för INTE OCH) sanningstabell och motsvarande NAND-grind. NAND-sanningstabellen och dess NAND-port är:
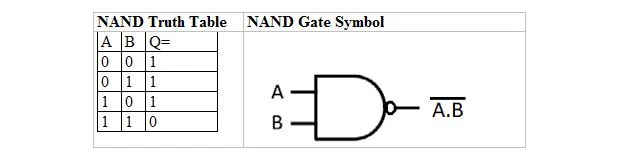
För att få NAND-sanningstabellen, gå till utgången av AND-sanningstabellen och ersätt varje siffra med dess komplement. Komplementet till 0 är 1 och komplementet till 1 är 0. NAND-grinden är som OCH-grinden, men har en liten cirkel före utgångslinjen. NAND-ekvationen är:
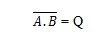
Där betyder komplementet till resultatet av 'A' OCH 'B'. Stapeln (överlinjen) representeras i porten av den lilla cirkeln. Observera att punkten mellan A och B kan utelämnas.
Det finns en annan sanningstabell och grind som härleds från OR-sanningstabellen och -porten. De kallas NOR (för INTE OR) sanningstabell och motsvarande NOR-port. NOR-sanningstabellen och dess NOR-port är:
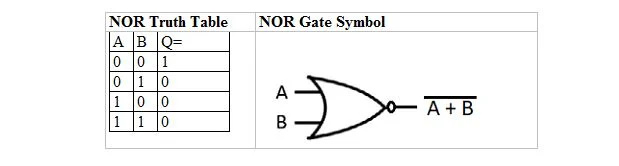
För att erhålla NOR-sanningstabellen, gå till utgången av OR-sanningstabellen och ersätt varje siffra med dess komplement. Komplementet av 0 är 1 och komplementet till 1 är 0. NOR-grinden är som OR-grinden, men har en liten cirkel före utgångslinjen. NOR-ekvationen är:
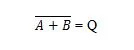
Var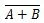 
betyder komplementet till resultatet av 'A' ELLER 'B'. Stapeln (överlinjen) representeras i porten av den lilla cirkeln.
Exklusiv ELLER (XOR)
Sanningstabellen för OR-porten är:
På normal engelska är det inte klart om den sista raden av 1 ELLER 1 ska ge 1 eller 0. Så i boolesk algebra finns det två sorters ELLER-sanningstabeller och två motsvarande grindar. Med det normala ELLER ger den sista raden av 1 ELLER 1 1. Den andra typen av ELLER är det exklusiva ELLER (XOR) där de tre första raderna är samma som de första tre raderna av normalt ELLER (inklusive utdata). Men för den fjärde och sista raden ger 1 ELLER 1 0.
Följande tabell ger XOR-sanningstabellen och dess XOR-gate (liten krets) symbol:
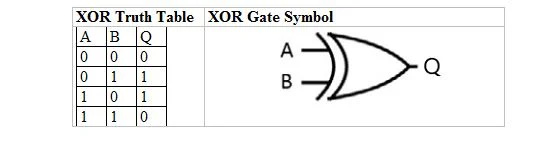
För både XOR-sanningstabellen och dess gate är 'A' såväl som 'B' två indatavariabler. 'Q' är utdatavariabeln.
XOR-ekvationen är:
A ⊕ B = Q
Där ⊕ här betyder Boolean XOR.
Det normala ELLER betyder endera eller båda. Exklusiv ELLER betyder strikt antingen och inte båda.
2.3 Booleska postulat
Postulat är antaganden baserade på vilka vissa slutsatser dras. Det finns tio booleska postulat som är baserade på OCH-, ELLER- och INTE-ekvationerna (sanningstabeller). Dessa ekvationer kallas även funktioner. De grundläggande funktionerna kopieras enligt följande:
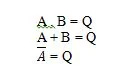
Dessa är de grundläggande funktionerna (ekvationerna) i boolesk algebra. Följande andra tre (funktions)ekvationer är inte grundläggande funktioner:
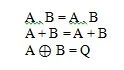
Även om den sista funktionen här är märklig, betraktas den inte som en grundläggande funktion.
De booleska postulaten är följande:
Från AND-funktion
1) 0 . 0 = 0
tjugo . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
Från ELLER-funktionen
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
Från NOT Function
9) 0 = 1
10) 1 = 0
Notera: Dessa postulat är bara linjerna i OCH, ELLER och INTE sanningstabellerna som uttrycks på ett oberoende sätt. Läsaren bör memorera de givna postulaten.
2.4 Booleska egenskaper
En egenskap är en liknande egenskap hos något. Booleska egenskaper är ekvationer som härleds från de booleska postulaten. I det här avsnittet ges egenskaperna helt enkelt utan deras härledningar och används sedan i efterhand. Det finns tjugofem av fastigheterna som är grupperade under tio rubriker enligt följande:
Egenskaper för OCH-funktionen
Egenskap 1:
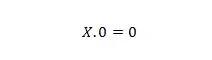
Där X kan vara 1 eller 0. Det betyder att oavsett vad X är så är resultatet alltid 0.
Obs: En variabel måste inte nödvändigtvis vara A eller B eller C eller D. En variabel kan vara W eller X eller Y eller Z eller någon annan bokstav.
Egendom 2:
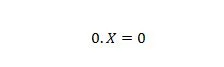
Där X kan vara 1 eller 0. Observera att skillnaden mellan egenskap 1 och egenskap 2 är att på vänster sida av likhetstecknet i båda ekvationerna, är positionerna för X och 0 utbytta.
Egenskap 3:
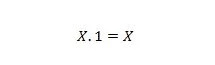
Om X är 0 så är 0. 1 = 0. Om X är 1 så är 1. 1 = 1.
Egendom 4:
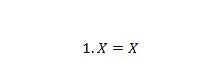
Om X är 0, då 1. 0 = 0. Om X är 1, då 1. 1 = 1. Observera att skillnaden mellan egenskap 3 och egenskap 4 är att på vänster sida av båda ekvationerna, positionerna för X och 1 är utbytta.
Egenskaper för ELLER-funktionen
Egendom 5:
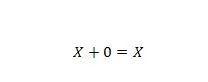
Där X kan vara 1 eller 0. Det betyder att om X är 0 är resultatet 0. Om X är 1 är resultatet 1.
Egendom 6:
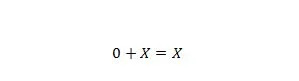
Där X kan vara 1 eller 0. Observera att skillnaden mellan egenskap 5 och egenskap 6 är att på vänster sida av båda ekvationerna är positionerna för X och 0 utbytta.
Egendom 7:
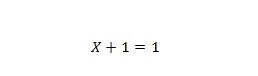
Om X är 0 så är 0 + 1 = 1. Om X är 1 så är 1 + 1 = 1.
Egendom 8:
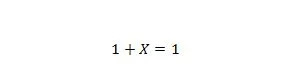
Om X är 0, då är 1 + 0 = 1. Om X är 1, då är 1 + 1 = 1. Observera att skillnaden mellan egenskap 7 och egenskap 8 är att på vänster sida av båda ekvationerna, positionerna för X och 1 är utbytta.
Egenskaper som gäller kombinationen av en variabel med sig själv eller dess komplement
Egendom 9: 
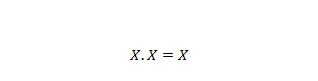
Det vill säga: om X är 0, då 0 . 0 = 0. Om X är 1, då 1 . 1 = 1.
Egendom 10:
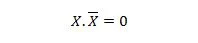
Det vill säga: om X är 0 så är 0. 1 = 0. Om X är 1 så är 1. 0 = 0.
För på varandra följande variabler blir denna egenskap:
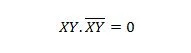
Egendom 11:
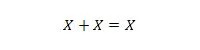
Det vill säga: om X är 0 så är 0 + 0 = 0. Om X är 1 så är 1 + 1 = 1 (från normal ELLER).
Egendom 12:
Det vill säga: om X är 0 så är 0 + 1 = 1. Om X = 1 så är 1 + 0 = 1.
Det vill säga: om X är 0 så är 0 + 1 = 1. Om X = 1 så är 1 + 0 = 1.
Dubbel komplementering
Egendom 13:
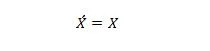
När X på vänster sida är 0, blir X på höger sida 0. När X på höger sida är 1, blir X på vänster sida 1. Med andra ord, dubbla komplement ger tillbaka det ursprungliga värdet.
Kommutativ lag
Egendom 14:
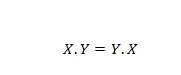
Detta betyder att det inte spelar någon roll att byta ut den första och den andra operanden för AND-operatorn på vänster sida av likhetstecknet; svaret är fortfarande detsamma efter att bytet på vänster sida har ägt rum. Denna ekvation kan skrivas med prickarna utelämnade som: XY = YX.
Egendom 15:
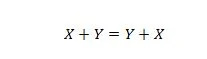
Förklaringen här är densamma som i föregående AND, men det är för OR-operatorn.
Distributiv lag
Fastighet 16:
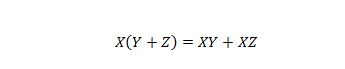
Här finns tre variabler: X, Y och Z. Varje variabel kan vara antingen 1 eller 0. På vänster sida av lika-symbolen betyder parenteserna att först utvärdera vad som finns i dem. Sedan är AND resultatet med X. Den högra sidan säger att X OCH Y tillsammans, ELLER X OCH Z tillsammans, är samma som vänstersidan. Observera att punktoperatorn för AND är utelämnad genomgående; och de sammanfogade variablerna betyder fortfarande OCH.
Fastighet 17:
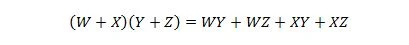
Denna egenskap är en förlängning av egenskap 16 med den tillagda variabeln W.
Associativ lag
Fastighet 18:
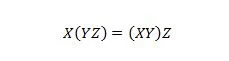
Parents betyder att först utvärdera vad som står inom parentes. Så, för uttrycket på vänster sida, om Y med Z är ANDed först, och X är ANDed med resultatet, då är det slutliga resultatet på vänster sida detsamma som det slutliga resultatet till höger -hand-sida där X med Y är ANDed först innan ANDing av resultatet med Z. Observera att prickarna har utelämnats i ekvationen.
Fastighet 19:
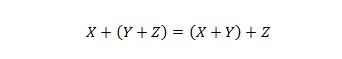
Denna egenskap förklaras på liknande sätt som egenskap 18, men ELLER-operatorn används istället för AND-operator. OR-operatorn + utelämnas aldrig från ett booleskt uttryck för enkelhetens skull. Å andra sidan kan AND-operatorn utelämnas och de två variablerna kan förenas.
Absorption
Fastighet 20:
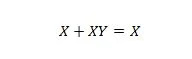
Med denna ekvation, oavsett vad Y är, kommer den högra sidan alltid att vara X (absorberad).
Fastighet 21:
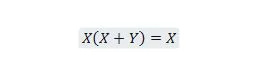
Med denna ekvation, oavsett vad Y är, kommer den högra sidan alltid att vara X (absorberad). Denna egenskap 21 är densamma som med egenskap 20 som är:
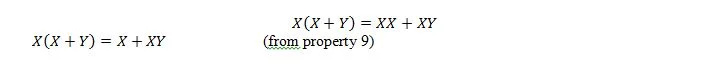
Här använder vi den fördelande lagen och det faktum att X.X = X av egendom 9.
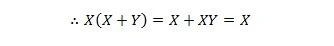
En identitet
Fastighet 22:
Detta betyder att för X + Y-uttrycket ändrar inte komplementet av X framför Y uttrycket.
Fastighet 23:
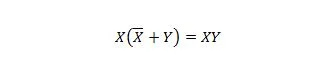
Detta betyder att för XY-uttrycket ändrar inte komplementet av X ORed med Y inom parentes, vilket görs först, XY-uttrycket.
DeMorgans lag
Fastighet 24:
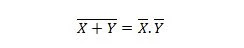
Detta betyder att en NOR (NOT OR)-grind har samma resultat som att NOTERA de två ingångarna innan AND-ing av dem.
Fastighet 25:
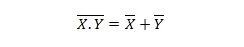
Detta betyder att en NAND (NOT AND)-grind har samma resultat som att NOTERA de två ingångarna före ELLER-ing.
De medföljande illustrationerna är de 25 fastigheterna. De kan bevisas genom att ersätta alla olika möjliga värden på 1:or och 0:or, i varje uttryck på vänster sida, för att se om uttrycket (eller resultatet) på höger sida erhålls. Bevisen lämnas som en övning för läsaren.
2.5 Förenkling av sammansatta uttryck
Följande två funktioner är desamma:
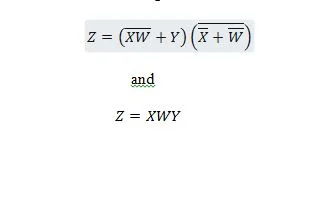
Z är utgången och X, W och Y är ingångarna. Den första behöver en NAND-grind, en ELLER-grind, en AND-grind, två INTE-grindar, en ELLER-grind och en NOR-grind. Den andra behöver bara två AND-grindar. Den första är en ekvation med ett sammansatt uttryck, på höger sida, som har förenklats (reducerats) till den enstaka högra uttryckstermen för den andra ekvationen.
Förenkling eller minskning leder till färre antal grindar för att implementera samma funktion som en krets. En sådan mindre krets kan vara en del av en Integrated Circuit (IC) eller vara en fristående krets på ytan av datorns moderkort.
När en funktion (ekvation) kommer fram till designprocessen måste förenkling ske för att minska antalet grindar och sluta med en billigare krets. Förenkling kräver användning av en eller flera av de tidigare tjugofem booleska egenskaperna.
Exempel 2.51:
Minska ekvationen:
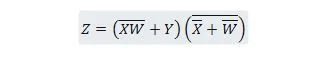
Notera: Två parenteser bredvid varandra betyder att parenteserna är ANDerade (punkten mellan dem har eventuellt inte skrivits).
Lösning:
För lösningarna anges motiveringen (anledning) för varje steg till höger om steget, inom parentes. Läsaren bör läsa varje steg och dess motivering. Läsaren bör också hänvisa till de tidigare egenskaperna när han/hon läser funktionsreduktionsstegen.
Exempel 2.52:
Förenkla:
2.6 Minsta summa av produkter
Följande två funktioner är desamma:
Båda högerhandsuttrycken av båda ekvationerna sägs vara i form av summan av produkter (SP). Ett uttryckligt uttryck sägs vara i summan av produktformen om det inte har parentes. Det är uppenbart att den första funktionen (ekvationen) behöver fler grindar än den andra funktionen.
Det första högeruttrycket kan fortfarande reduceras för att få den andra funktionen. Det andra uttrycket på höger sida kan inte förenklas ytterligare och kan fortfarande uttryckas som summan av produkter (”tillägg” av termer). Det andra uttrycket på höger sida kan egentligen inte förenklas ytterligare. Så det sägs vara i formen Minimum Sum of Products (MSP).
Exempel 2.61:
Ta med följande funktion först till formuläret Summa av produkter och sedan till formuläret Minsta summa av produkter.
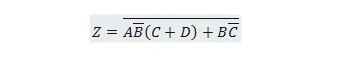
Lösning:
När man löser problem som detta måste en eller flera av de tidigare tjugofem egenskaperna användas som illustreras i denna lösning:
2.6 Minsta summa av produkter
Följande två funktioner är desamma:
Båda högerhandsuttrycken av båda ekvationerna sägs vara i form av summan av produkter (SP). Ett uttryckligt uttryck sägs vara i summan av produktformen om det inte har parentes. Det är uppenbart att den första funktionen (ekvationen) behöver fler grindar än den andra funktionen.
Det första högeruttrycket kan fortfarande reduceras för att få den andra funktionen. Det andra uttrycket på höger sida kan inte förenklas ytterligare och fortfarande uttryckas som summan av produkter (”tillägg” av termer). Det andra uttrycket på höger sida kan egentligen inte förenklas ytterligare. Så det sägs vara i formen Minimum Sum of Products (MSP).
Exempel 2.61:
Ta med följande funktion först till formuläret Summa av produkter och sedan till formuläret Minsta summa av produkter.
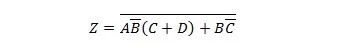
Lösning:
När man löser problem som detta måste en eller flera av de tidigare tjugofem egenskaperna användas som illustreras i denna lösning:
Det sista uttrycket är i formen Sum of Products (SP), men inte i formen Minimum Sum of Products (MSP). Den första delen av frågan har besvarats. Lösningen för den andra delen är som följer:
Denna sista förenklade funktion (ekvation) är i MSP-form och behöver mindre antal grindar för implementering än dess motsvarande SP-form. Kom ihåg: SP betyder summan av produkter medan MSP betyder minsta summan av produkter.
Exempel 2.62:
Följande krets har X-, Y- och W-ingångarna och Z är utgången. Producera funktionen Sum of Products (SP) (skenbar minsta summa av produkters funktion) för Z. Ta sedan fram den verkliga mer reducerade (minimerade) Summan av produkter (MSP). Implementera sedan MSP-kretsen (rita MSP-grindningsnätverket).
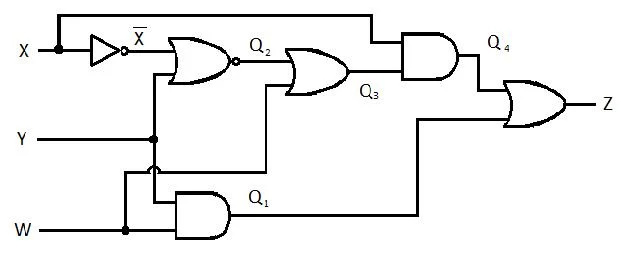
Fig 2.61 En grindkrets
Lösning:
Innan förenklingsprocessen startar måste uttrycket för Z fås i termer av X, Y och W. Se denna exempelillustration från diagrammet:
Detta är uttrycket för Z i termer av X, Y och W. Efter detta kan förenklingen till skenbar MSP ske. Uppenbarligen är MSP SP.
Denna sista ekvation (funktion) är i SP-form. Det är inte sant minimumsumma av produkter (ännu inte MSP). Så minskningen (minimeringen) måste fortsätta.
Denna sista ekvation (funktion) är en sann minimumsumma av produkter (MSP). Och minimisumman av produkter (verklig minimering) grindkrets är:
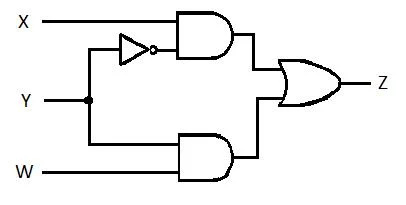
Fig 2.62 MSP-portkrets
Kommentar
Av analysen i detta avsnitt kan man se att det inte är klart om summan av produkter är minimisumman av produkter eller inte. SP är inte särskilt användbart. Det är MSP som är väldigt användbart. Det finns ett säkert sätt att få MSP; det är att använda Karnaugh-kartan. Karnaugh Map ligger utanför ramen för denna online karriärkurs.
2.7 Problem
Läsaren rekommenderas att lösa alla problem i ett kapitel innan du går vidare till nästa kapitel.
- Skapa sanningstabellerna OCH, ELLER och INTE med motsvarande grindar.
- Skriv ner de tio booleska postulaten i deras olika kategorier och namnge kategorierna.
- Utan förklaring, skriv ner de tjugosex egenskaperna för boolesk algebra i deras olika kategorier och namnge kategorierna.
- Minska ekvationen med hjälp av de booleska egenskaperna och citera de använda kategorierna.
- Minska ekvationen med hjälp av de booleska egenskaperna och citera de använda kategorierna.
- Använd de booleska egenskaperna och citera de använda kategorierna, reducera följande ekvation – först till summan av produkter och sedan till minsta summan av produkter:
- Använd de booleska egenskaperna och citera de använda kategorierna, reducera följande ekvation – först till summan av produkter och sedan till minsta summan av produkter:
